Rsa暗号 問題点
, rsa 暗号を解読する 方法は見つ かっ ていない ことから , 素因数分解問 題は , rsa 暗号の安全性の根拠であるとされて い る.ただし,rsa 暗号の安全性が真に素因数 分解問題と本当に等価であるかどうかにつ いては, 現時点でまだ示されてい ない. 3.

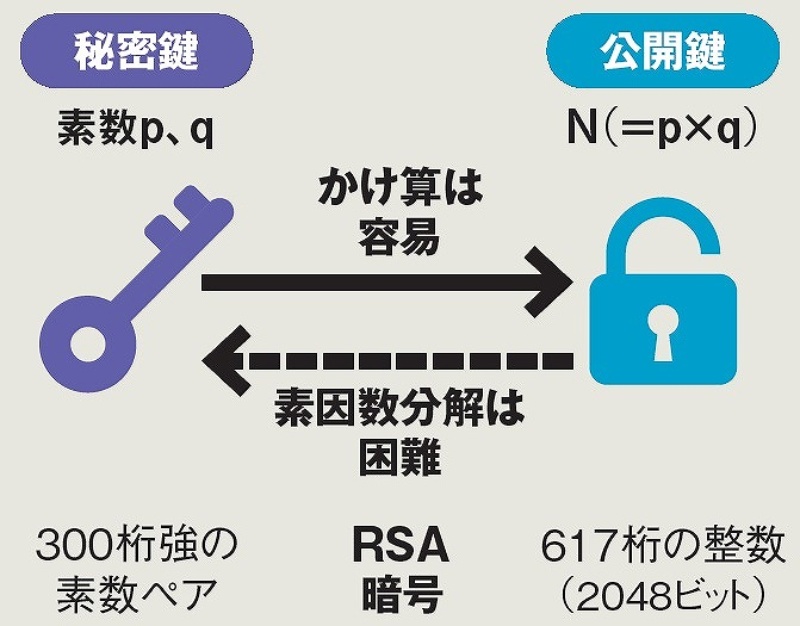
Rsa暗号 問題点. では、なぜ、公開鍵から秘密鍵がばれてしまうという、暗号としては致命的とも思われる欠点を持つ、rsa暗号が使われているかというと… まず、現在では、暗号の研究と、「計算機」の高性能化が非常に進んでいて、 素人考えの暗号では、すでに秘密を守れない 、ということがあります。. RSA暗号とは、桁数が大きい合成数の素因数分解問題が困難であることを安全性の根拠とした公開鍵暗号の一つである。 -- RSA暗号 - Wikipedia より RSAでは N には桁数が大きい素数 p 、 q の合成数を選択します φ (n) を計算するためには、素因数分解が必要となる. かどうかを判定する方法としては非実用的である.実は,rsa暗号を使うためには,非常 に大きな素数を用意しなければならないため,この問題は実は重要である. さて,素数を使って述べられる性質として最も重要なものは素因数分解である. 定理2.2.
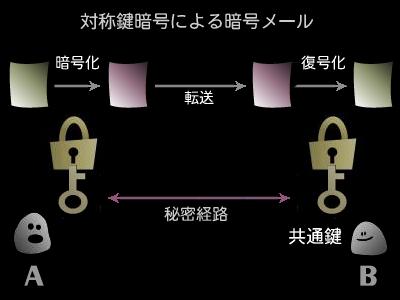
林:準同型暗号を用いた秘密計算とその応用 65 間とする.Encを確率的な暗号化関数,Decを決定的な 復号関数とし,メッセージm∈M について,暗号化を c←Enc(m,pk) とし,その復号をm←Dec(c,sk) とす る.ここで,「暗号化したままデータを処理できる」とは,. 共通鍵暗号の場合,あらかじめ送信者と受信者で共通鍵を共有しておく必要があります。 悪いやつに盗み見られても復号できないために暗号化を用いるのに, あらかじめ他人にバレないように共通鍵を共有する という行為が矛盾して. 格子問題(lwe 問題等) ⁃ 符号に基づく暗号:.
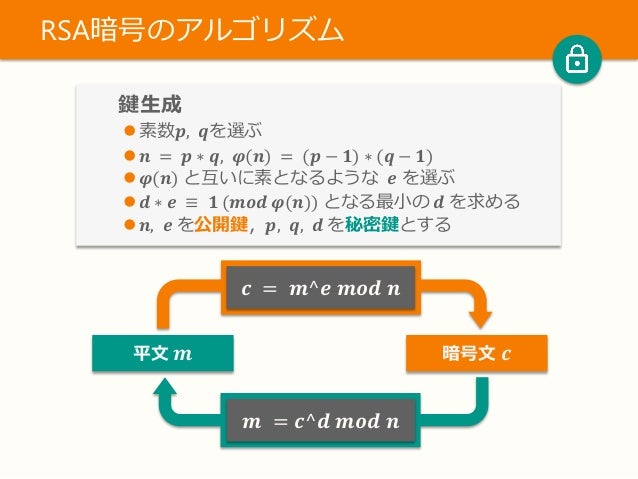
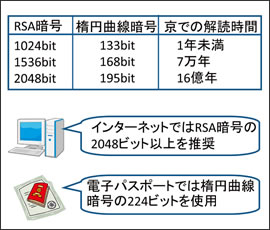
楕円曲線暗号は,楕円曲線上の点演算を用いて暗号 化する.この点演算は離散対数問題に帰着される一方 向性関数であり,rsaなどに比べて短い鍵長で高い安 全性が得られる.たとえば,鍵長173ビットの楕円曲 線暗号は,鍵長1024ビットのrsa暗号と同等である.. Mp 問題, ip 問題. RSA 暗号 Rivest, Shamir, Adleman により考案された(1977) 前述の要件を満たす暗号方式の一つ 公開鍵n は素数p;q を2 つかけたもの(n = pq) 例:.
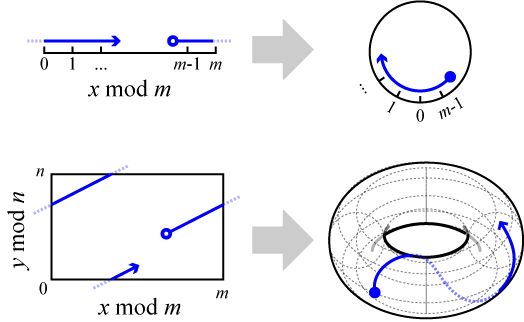
1024ビットRSA 暗号の公開鍵は, 150桁程度の素 数を2 つかけたもの 0 ≤x ≤n−1 なる整数x を, 同じ範囲の整数に変換, 逆 変換できる. 楕円曲線上の離散対数問題 • pqc として期待される公開鍵暗号 ⁃ 格子に基づく暗号:. 楕円曲線暗号ECC / Elliptic Curve Cryptographyとは、楕円曲線上の離散対数問題と呼ばれる数学上の問題を安全性の根拠とする暗号。1985年に暗号学者のビクター・ミラー(Victor Miller)氏とニール・コブリッツ(Neal Koblitz)氏が独立のほぼ同時に考案した。具体的な暗号方式として楕円曲線DSA(ECDSA)や楕円.
共通鍵暗号 3.共通鍵暗号方式の問題点 4.公開鍵暗号方式 5.公開鍵暗号方式のデジタル署名への適用 6.sshで公開鍵認証を使った認証手順. 公開鍵暗号のメリット・デメリット 共通鍵暗号のデメリットを解決する概念、「公開鍵暗号」について。 もちろん、メリットとデメリットがありますので、共通鍵暗号のときと同様ご紹介します。 公開鍵暗号のメリット 公開鍵暗号のメリットは、その堅牢性です。. RSA の計算例 さて,準備が整ったところで暗号化をしましょう。今から 1371 (cat という文字列を数値化したもの)を暗号化します。 まず,かけ算すると 1371 より大きくなるような二つの素数を適当に選んできます。.
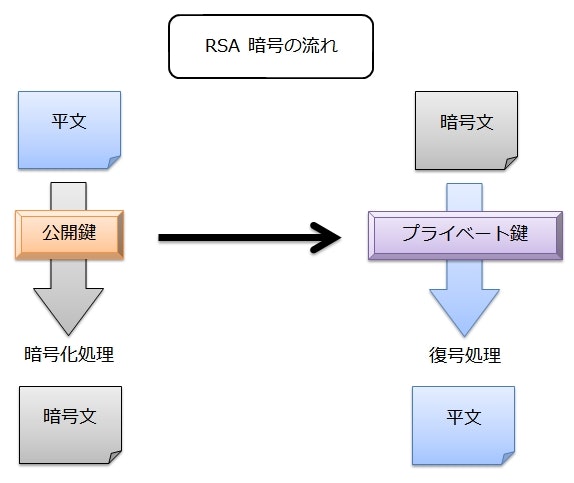
1.4 rsa暗号の教材化に関する問題点と解決策 これまでrsa暗号が教材として扱われてきたが,次 のような問題点があった。 ・暗号化や復号する際の計算が複雑であり,電卓で は計算できない。 ・平文として大きな数を扱うには,大きな素数と鍵. Javaでrsa暗号を使う際にcryptrec暗号リストに足元をすくわれる可能性を回避する 投稿日:19年6月27日 更新日: 19年7月24日 標準的な暗号しか使わないケースでもJavaでRSAを使う時はBouncyCastleを入れておいた方が無難、という話です。. 公開鍵暗号方式はみんなが知っている鍵で暗号化し、自分だけが知っている鍵で復号しますよね。 rsa暗号は数学を用いてそれを可能にしています。 その方法はすごく 簡単なのに斬新 です!!!私は考えた人をマジな天才だと思っています。.
– 代表的な共通鍵暗号 DES, AES, MISTY, Camellia • 公開鍵暗号(非対称鍵暗号) – public key とprivate key を用いる:public key は公開 – ディジタル署名や鍵配送など応用が豊富、但し低速 – 公開鍵暗号の現在の主流はRSA暗号. Rsa暗号 概要 今日は有名なrsa暗号問題について見ていきたい。 rsa暗号とは. 楕円曲線暗号とRSA 暗号の安全性比較y 富士通株式会社, 株式会社富士通研究所 10年8月日 概要 本稿では、楕円曲線離散対数問題に関して実施した計算機実験に基づく計算量評価ならびに従来知られて.
Adleman, “A method for obtaining digital signatures and public-key cryptosystem,” Communications of th ACM, 21(1978), pp.1 -126, 1978. Des暗号やrsa暗号の問題点ってなんですか?? des暗号とrsa暗号の違いなどもわからないんですが。。。 とりあえず、問題点について調べてるんでお願いします。 何もわからないので 基礎を簡単におね車に関する質問ならgoo知恵袋。あなたの質問に50万人以上のユーザーが回答を寄せてくれます。. Lpn 問題 ⁃ 多変数多項式に基づく暗号:.
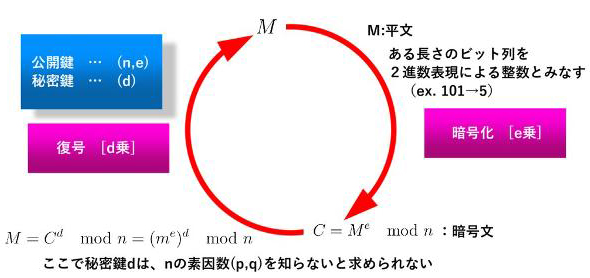
RSA暗号の安全性 • 公開鍵nが素因数分解されるとp,qが求まる。 • 公開鍵eから、関係式 d =1/e mod (p-1)(q-1) により、秘密鍵dを求めることができる。 •RSA暗号の安全性は、素因数分解の困難性 に根拠を置いている。 15/28. Python 3.7.1 「RSA暗号クイズ」の制作 問題について.

電子署名と公開鍵暗号方式 電子署名 認証センター

暗号の数学的基礎 数論とrsa暗号入門 S C コウチーニョ Coutinho S C 彬 林 本 通販 Amazon

公開鍵暗号 D Space アットウィキ
Rsa暗号 問題点 のギャラリー
Nict News

2つの公開鍵暗号 公開鍵暗号の基礎知識 Qiita

Rsa暗号運用でやってはいけない N のこと Ssmjp
R Rsa暗号を使ってみる クイックノート

Rsa暗号の仕組み 証明 合同式とrsa暗号 第9回 Youtube

Vnvt Uf 7hz5xm

Rsa暗号運用でやってはいけない N のこと Ssmjp

公開鍵暗号システム Rsa暗号 8分 おまけ5分 Youtube

グーグル 48ビットrsa暗号化キーへのアップグレードを完了 Cnet Japan

視覚的にイメージしにくいアルゴリズムを徹底的にイラストで表現するとこうなる 3 4 Codezine コードジン
世界初 60次元の格子暗号を解読 九州大学 理学研究院 理学府 理学部
量子コンピュータによる暗号解読の可能性 Nttデータ
楕円曲線暗号 Moxbox

Lineは48ビットrsa採用 暗号化が弱いためデータ流出の可能性 は 誤解 と技術ブログで説明 Itmedia News

Rsa 暗号がようやく分かった気がしたのでまとめてみる Tsujimotterのノートブック

1999 1436号 演算装置並びにこれを利用したrsa暗号演算装置及び楕円暗号演算装置 Astamuse
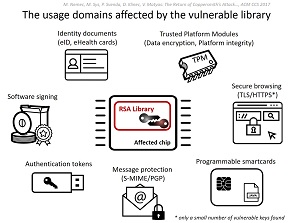
セキュリティチップにrsa暗号鍵の脆弱性 Googleやmicrosoftの製品にも影響 Itmedia エンタープライズ
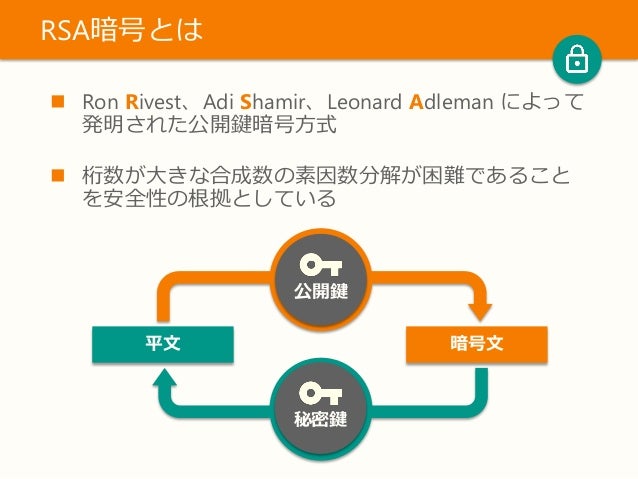
Rsa暗号運用でやってはいけない N のこと Ssmjp
2

基礎から学ぶ整数論 Rsa暗号入門 コロナ社
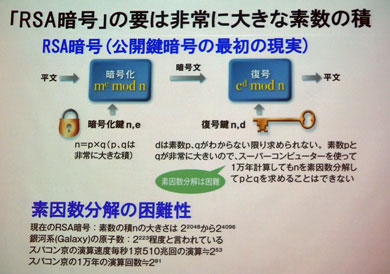
国際科学技術財団 日本国際賞 にrsa暗号開発のアディ シャミア氏を選出 Itmedia エンタープライズ

Rsa暗号
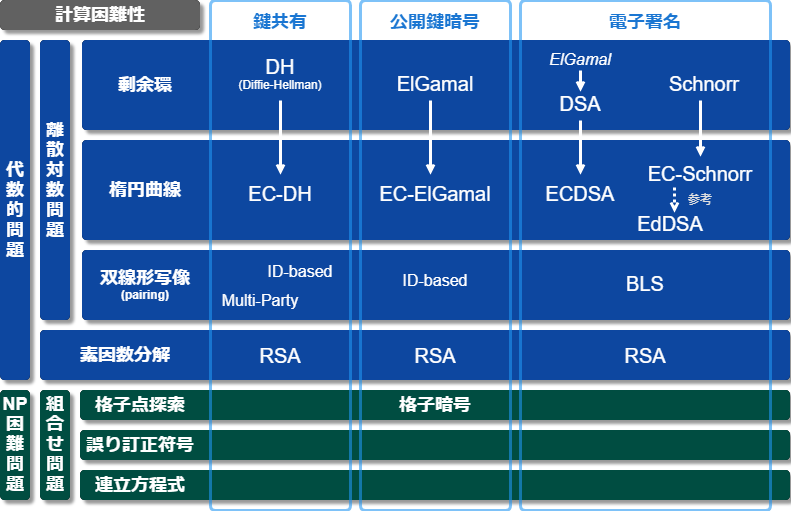
公開鍵暗号アルゴリズム Moxbox
Http Www Ie U Ryukyu Ac Jp Wada Cad07 Dwm Pdf
量子コンピューターが暗号技術を 破壊 する その真偽を検証してみた 日経クロステック Xtech
暗号技術勉強メモ Qiita
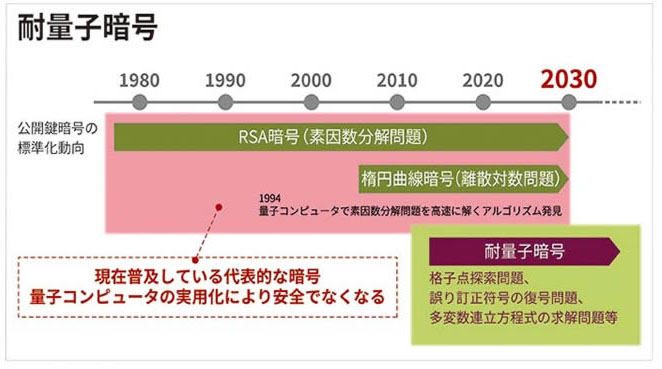
量子コンピュータの実用化と耐量子暗号の標準化動向 Sqat Jp

Rsaの公開鍵暗号のアルゴリズム4つ Rsa暗号の安全性について2つ テックマガジン From Fenetインフラ
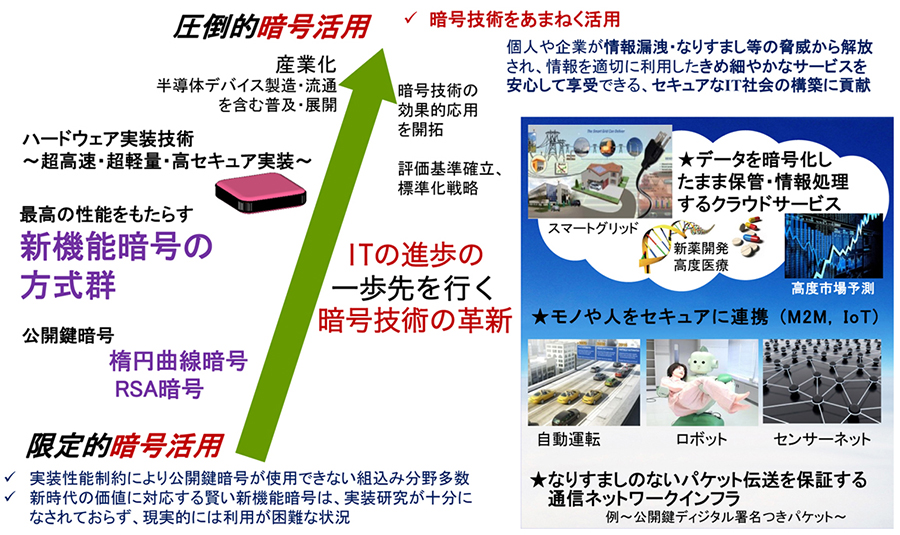
助成研究者情報 松本勉先生2 安全安心な科学技術の振興 セコム科学技術振興財団

Rsa暗号運用でやってはいけない N のこと Ssmjp

Rsa暗号のしくみ Qiita

連載 暗号と暗号史 第8回 有史以来の課題を解決 公開鍵暗号 Rsa暗号 Hh News Reports ハミングヘッズ
失礼します Rsa暗号の解き方をお願いします 興味本位で Yahoo 知恵袋

公開鍵暗号 D Space アットウィキ

暗号コラム 実験室 先進ict研究開発支援サービス

Rsa暗号運用でやってはいけない N のこと Ssmjp

Ppt Rsa 暗号の多変数化と 連立代数方程式 Powerpoint Presentation Id
Rsa暗号運用でやってはいけない N のこと Ssmjp

連載 暗号と暗号史 第8回 有史以来の課題を解決 公開鍵暗号 Rsa暗号 Hh News Reports ハミングヘッズ

しょうがくせい向けrsa暗号の仕組み
Gnupg 0
Webの信用と鍵の寿命 デジタル時代のhanko 公開鍵暗号の実装変更 Rsa Ed Dxgov Js Opendata 福野泰介の一日一創 Create Every Day By Taisuke Fukuno

暗号化通信を解読される Freak 脆弱性 Windowsも影響を受ける 日経クロステック Xtech
Rsaとは Rsa暗号とは It

暗号の数学的基礎 丸善出版 理工 医学 人文社会科学の専門書出版社
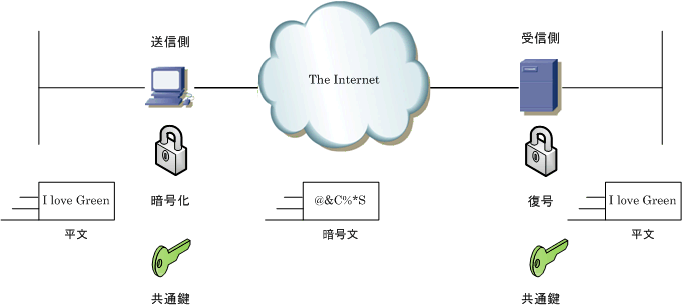
共通鍵暗号と公開鍵暗号とは

Rsa暗号運用でやってはいけない N のこと Ssmjp

S19 011 量子コンピュータと暗号化手法 Itセキュリティ対策 豆知識

グーグル 48ビットrsa暗号化キーへのアップグレードを完了 Cnet Japan
Nict News
Http Www Ms U Tokyo Ac Jp Tambara Docs L4h1728 2takagi Pdf

電子署名と公開鍵暗号方式 電子署名 認証センター
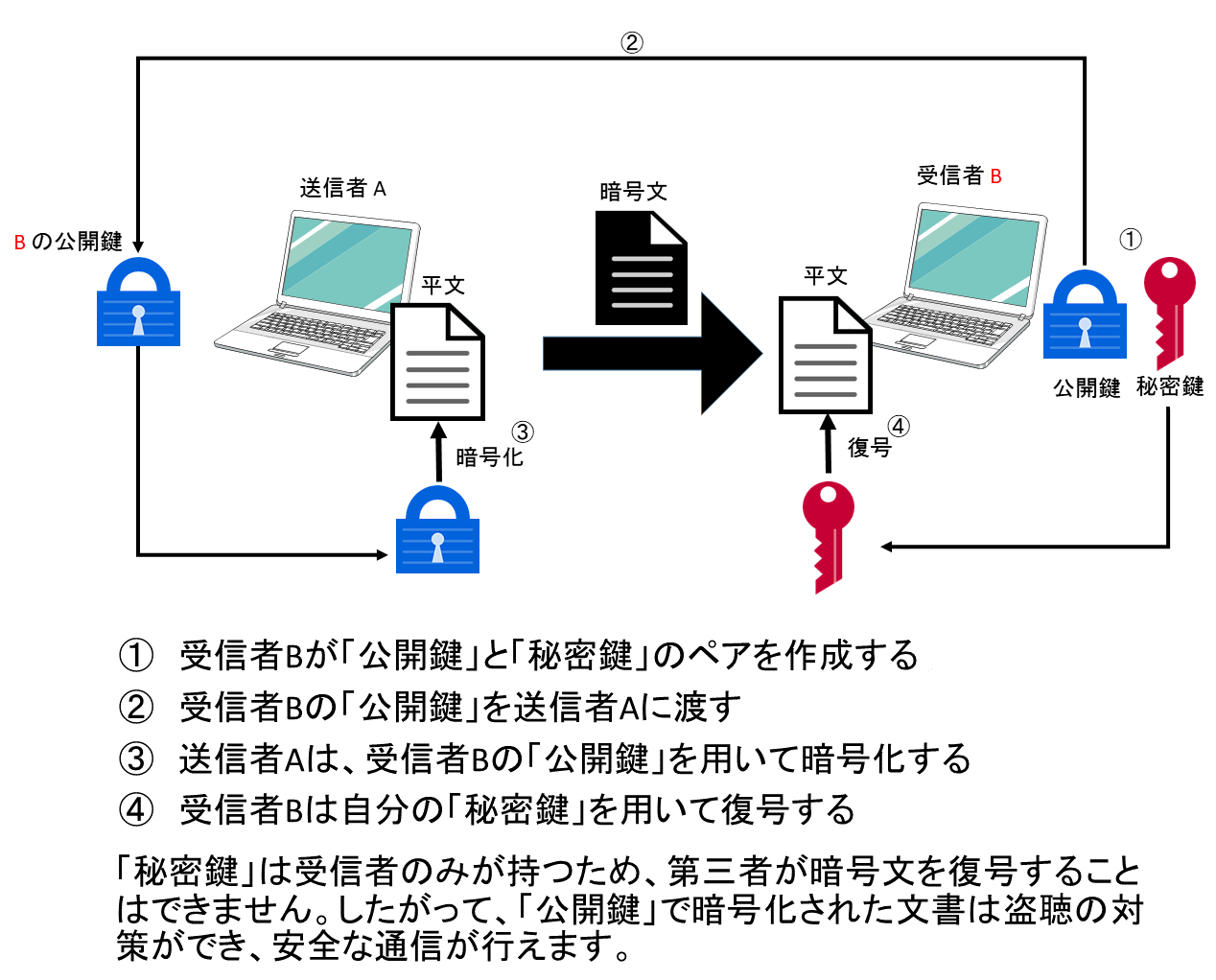
暗号技術の基礎固め Think It シンクイット

Rsa暗号ってどういうしくみなの Qiita

数学が役に立っている Rsa暗号の仕組みを解説 合同式とrsa暗号 第8回 Youtube
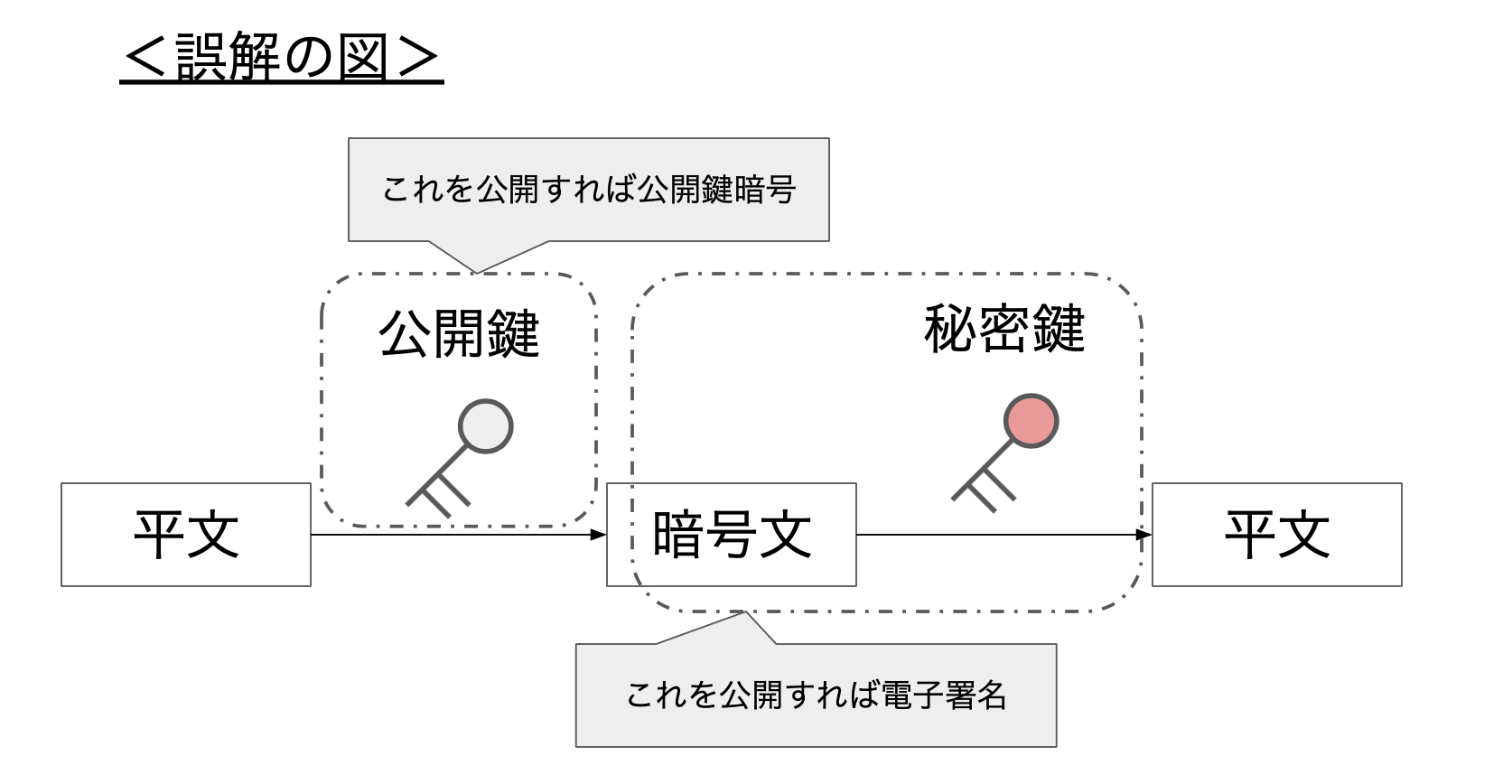
私は公開鍵暗号方式と電子署名を理解できていなかったようです まえおき By Hashhub Space Gbec Tech Blog Medium

Rsa暗号の仕組みとは 作り方や解き方 安全性までわかりやすく解説します 遊ぶ数学

Rsa暗号の仕組みとは 作り方や解き方 安全性までわかりやすく解説します 遊ぶ数学

Rsa暗号ってなに Runtime

暗号のしくみと素因数分解 その2 9 11更新 Rsa暗号のアルゴリズム 象が転んだ
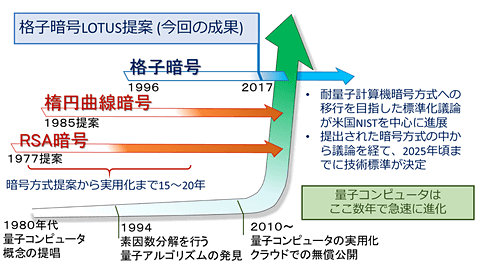
量子コンピュータでも解読が困難な新暗号方式が国内で開発 Pc Watch
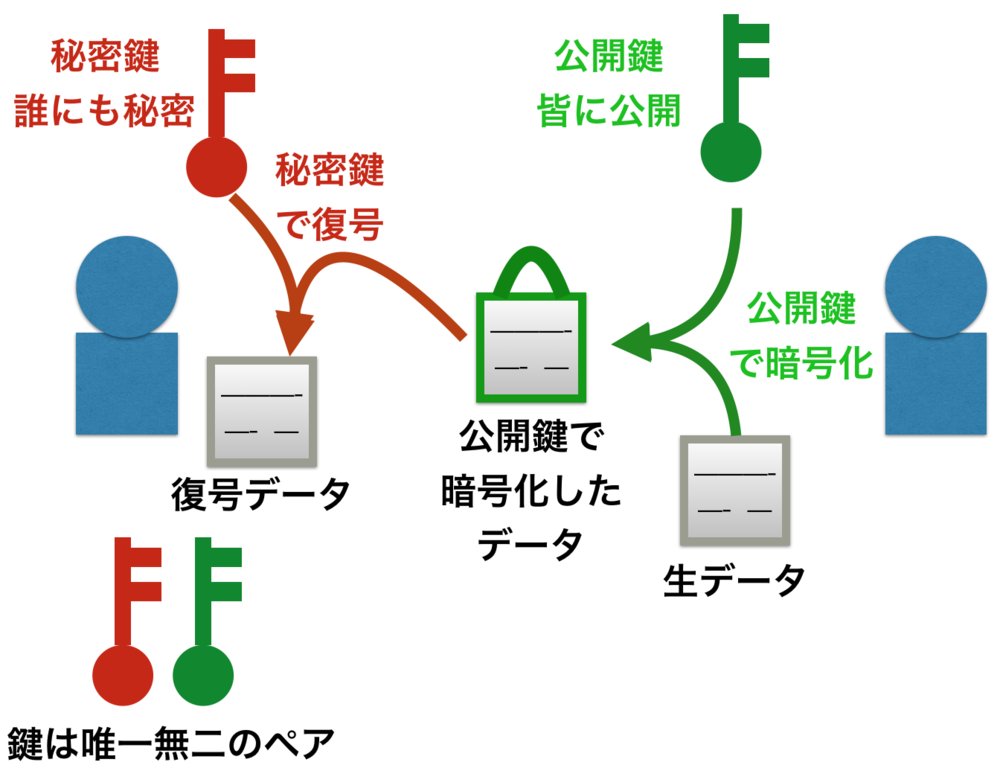
公開鍵暗号方式とは Thoth Children
Http Www3 Muroran It Ac Jp C Prog Cryptography 2 Pdf

Rsa暗号解読問題を解く 後編 Ctf For Beginners 18 Rsa Is Power Mawalog

セキュリティチップにrsa暗号鍵の脆弱性 Googleやmicrosoftの製品にも影響 Itmedia エンタープライズ

Basic 14 暗号について Rsa 暗号 楕円曲線暗号

公開鍵暗号rsaの数的構造 Qiita

先端暗号技術入門コース 量子コンピュータと共に変容する暗号技術の基礎と応用 開発課題 R2 Kistec 地方独立行政法人 神奈川県立産業技術総合研究所
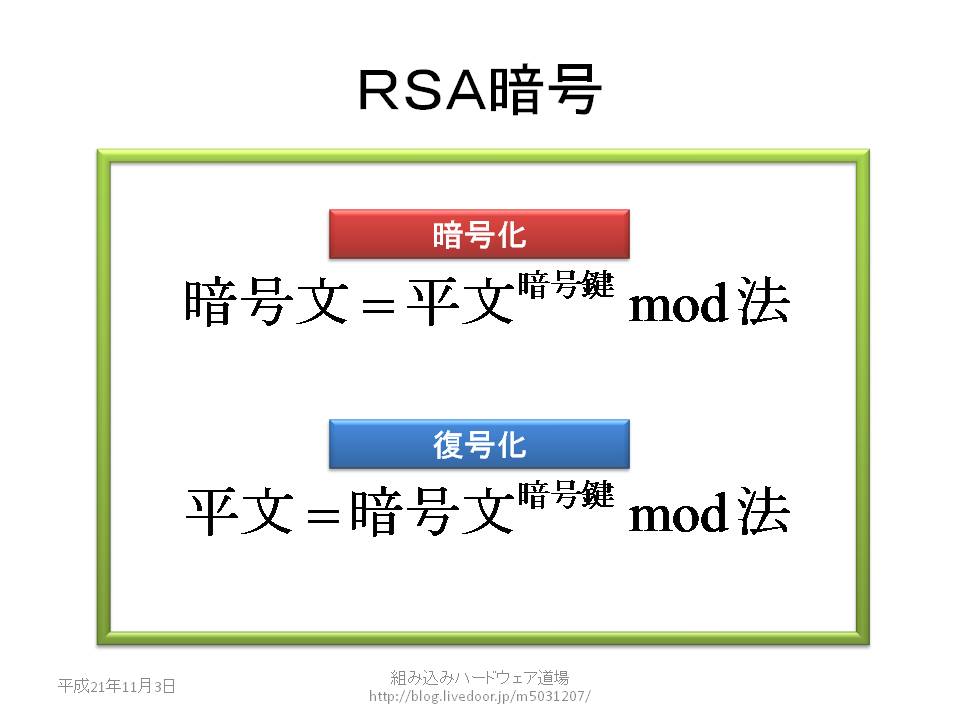
Rsa暗号とは 組み込みハードウェア道場
Www Nict Go Jp Data Nict News Nict News 19 474 J Pdf
Rsa暗号 弊研究室の某課題について考える日目 ごちうさ民の覚え書き
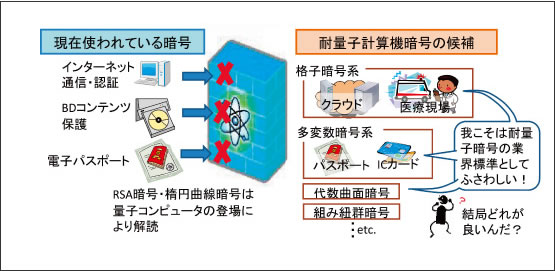
Nict News
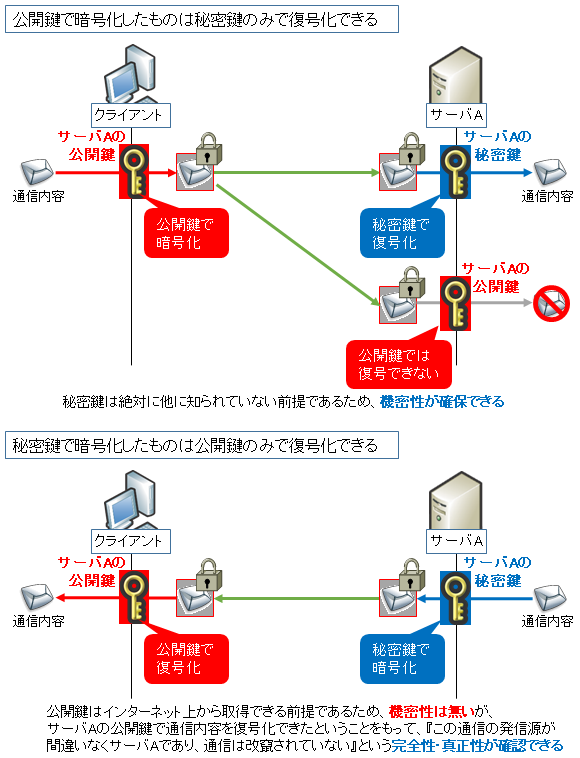
図解 初心者も分かる 公開鍵 秘密鍵 の仕組み 公開鍵暗号方式の身近で具体的な利用例やメリット Seの道標
公開鍵暗号 Rsa 基礎 ง W ว 暗号楽しいです
/pic311.jpg)
テクノインテリジェンス

Nict News

Rsaをはじめとした暗号化の仕組みと方式の違いとは マルウェア情報局
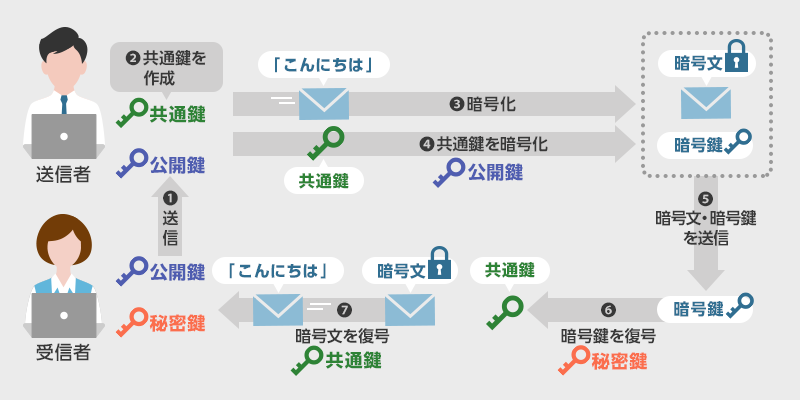
Rsaをはじめとした暗号化の仕組みと方式の違いとは マルウェア情報局

数学が役に立っている Rsa暗号の仕組みを解説 合同式とrsa暗号 第8回 Youtube

サマーウォーズの暗号は京大生レベルの数学でも解けるのか

Des Rsa暗号に関する計算問題 演習 レポート課題 と似た問題は出題しません Ppt Download
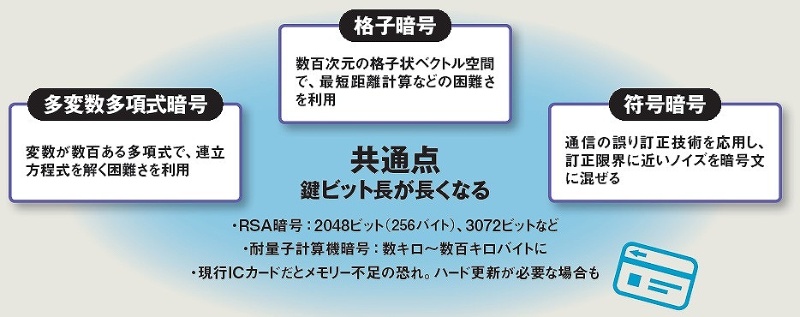
量子コンピューターでも破れない次世代暗号 日米で進む標準化の最新動向 日経クロステック Xtech

Rsa暗号とは 仕組みをわかりやすく解説 プログラム付き じゃぱざむ

Bkpctfのrsa暗号問題を解く Sonickun Log

暗号化のメリットとデメリットは 注意するポイントも Itトレンド

Rsa暗号運用でやってはいけない N のこと Ssmjp

Rsa暗号の原理
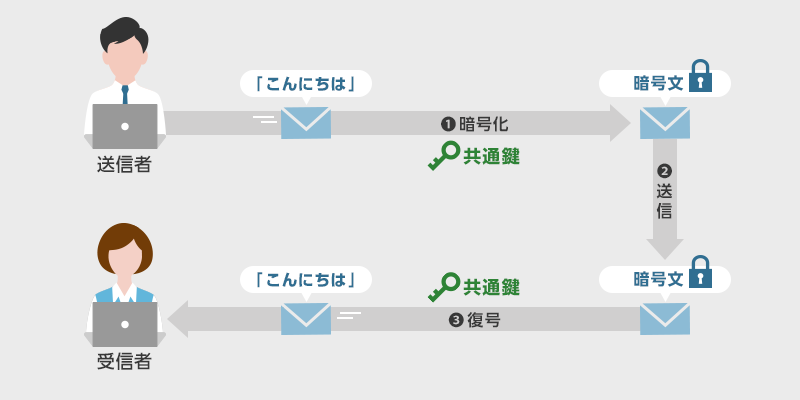
Rsaをはじめとした暗号化の仕組みと方式の違いとは マルウェア情報局
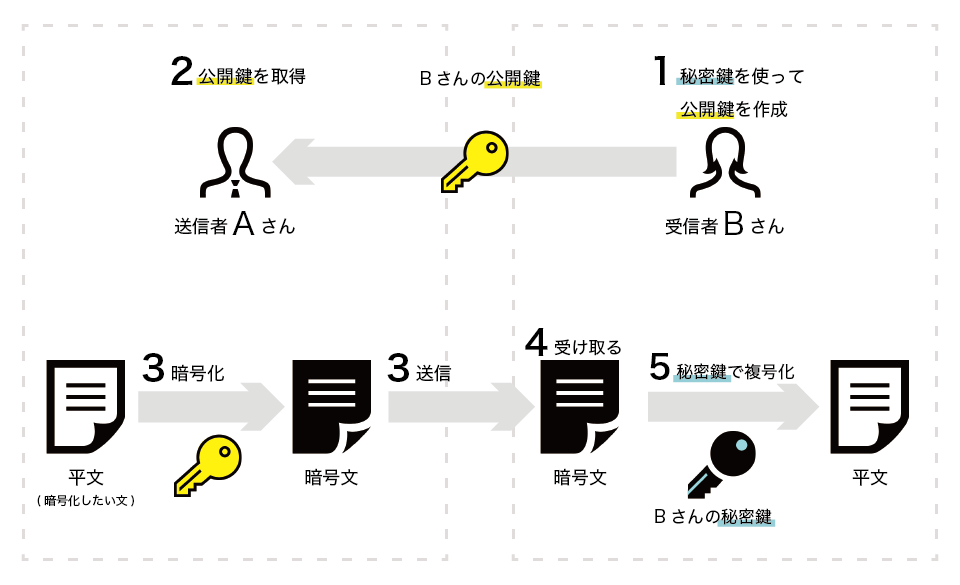
公開鍵暗号方式とは 初心者でもわかる公開鍵暗号方式の基礎 Udemy メディア

Pki関連技術に関するコンテンツ

Rsa暗号からの脱出 Tsujimotterのノートブック

Rsaの公開鍵暗号のアルゴリズム4つ Rsa暗号の安全性について2つ テックマガジン From Fenetインフラ

Rsa暗号と量子コンピューティング 公開鍵暗号方式のおさらい Qiita
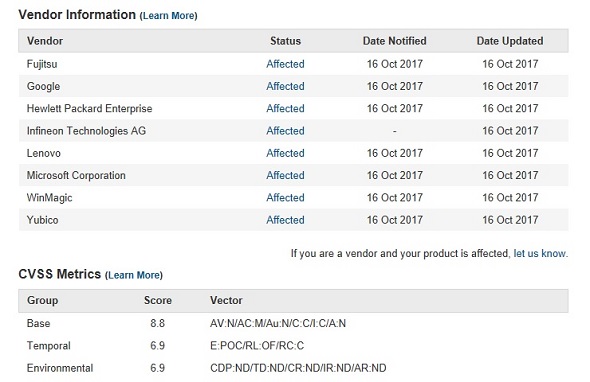
セキュリティチップにrsa暗号鍵の脆弱性 Googleやmicrosoftの製品にも影響 Itmedia エンタープライズ
Rsa暗号 解き方 Qoelizabethou87 S Diary
本気で考えてみた サマーウォーズのパスワードの暗号の解き方 56桁の暗号は解けるのか ぐだぐだプログラム日記

Rsa の計算例




